人工智能背景下高等数学课程的教学案例研究

张倩铃 肖梅
（四川旅游学院，四川成都 610100）

摘要：在人工智能和数字教育背景下，高等数学教学方法正经历深刻变革。本文以高校本科生为研究对象，基于超星学习通平台完成高等数学中函数连续性的线上+线下课程的混合式教学设计，实现教师为引领，学生为主体的互动教学模式，通过实例导入与主体能动性，提升学生自主学习能力，激发学生学习兴趣，结合小组互助与成果展示，为课堂注入活力。
关键词：人工智能；教学案例；函数连续性

引言：

随着 ChatGPT 大模型的横空出世，迎来了面向人类的文本对话，豆包、deepseek、讯飞星火、文心一言等软件的广泛应用，正改变着人们传统的工作学习方式。文献写到科学和技术是改变人类生活的重要因素，它既改变了人类生活活动的形式，也改变了人类生活的行为特征。

作为高校数学类课程教师，面对学生来源的多样化和层次的差异化，给高等数学教学带来了新的挑战和亟待解决的新问题，如学生缺乏学习兴趣、没有处理好高等数学和专业课程之间的关系。以“人工智能的应用”为主题，在知网检索出相关文献 6.79 万篇，进一步检索出关于“在教学中的

应用”文献 714 篇，主要从教学模式改革、思政元素融合、案例研究等混合式教学的视角出发涵盖了外语、医学、音乐、计算机等学科专业，人工智能助力新时代教学。

一、文献综述

人工智能背景下，高等数学课程教学模式的创新研究较多。文献以“立德树人、启智致用、交叉融合”为理念，开发人工智能+高等数学融合的课程，以“传道+授业+解惑+ 启智+致用”分层递进五个层次构建高等数学课程教学模式教学体系，达到培养创新型、应用型、的复合人才；作者对比 ChatGPT 和人对一元微积分例题求解的准确率和平均速度，探讨生成式人工智能对教育环节、学习空间、学习内容、学习评价、学习模式的冲击，建立新的教学结构链、设计新的学习背景、尝试沉浸式个性化学习模式，把控基于生成式人工智能的学习质量、构建公平科学的评价体系、培养思辨性创新型人才；黄利文等人以数据为驱动探讨课堂教学情况、教学内容片段资源库建设、学业诊断和个性化学习的教学育人模式。

为深化教育理论研究，关于高等数学的教学案例不断涌现。龚薇等人以函数连续性的教学过程为例，采用混合式教学进行教学设计，融入思政元素，丰富了教学内容，拓展了课程的高阶性、创新性和挑战度，提高了学生学习的积极性，提升了课程教学质量，实现课程教学创新与课程育人的双重目标。沈小雨以微积分为例从教学框架、挑战与应用、多方评价的角度探讨了在 AI 技术下的项目式学习。本文在前人研究的基础上，基于超星学习通平台，以高等数学中函数的连续性为例探究混合式教学模式。

二、在人工智能背景下的混合式教学设计

1.课前准备
一堂课程的呈现跟老师的备课有直接的关系。在立德树人的教学理念下，备课过程中从数学史和知识点两方面深挖课程思政，达到教授知识和育人的目的，传递知识的产生不是一朝一夕的，是在数学家的坚持不懈和多年的沉淀下形成的，培养学生勇于探索不怕失败的精神。闭区间上的连续函数具有最值、有界性、介值性等性质，在高等数学中是比较重要的概念。在预备函数连续性这节内容时，查阅到是 17世纪欧洲数学家如斯奈尔首先对函数连续性进行初步探索，到 19 世纪柯西等数学家在微积分研究中深入探讨并作出完美定义和性质分析，连续性概念在数学界引起了轰动，函数连续性的萌芽到发展再到应用，历经 3 个世纪之久，多位数学家不断探索和知识迭代中形成的，体现数学家对生活问题的洞察和对数学的热爱。

还需要对学生的学习情况作分析，面向讲授对象的专业特点、前期学习情况和知识基础、学生的生理和心理特征、学生的学习能力和学习态度等，掌握讲授班级学生的学习情况，可以帮助老师选择合适的教学风格和方式，实现学生学习和教师讲授的合一，提高课堂教学效率。以四川某高校24 级 3 班食品科学与工程专业的 36 名学生作为授课对象，从人才培养计划了解本课程是该专业的专业基础必修课程，大一第一学期和第二学期总计 96 学时，涵盖了极限分析在特定时间或条件下描述微生物数量的变化趋势，运用食品质地的应力-应变曲线导数计算食品的弹性模量等参数，为保证食品品质利用积分曲线计算加热或冷却过程中食品吸收或释放的热量等内容。本班级人物特征，男生 13 人，女生23 人，年龄在 17~19 岁，青少年时期随着身体发展的完善，认知、思维能力处在高峰期，在理科生背景的基础上，对高等数学知识的接受程度较高，同时，学生沿袭高中学习的积极性和踏实度，有利推进课程教学。

此外，教学内容与生活实例相结合，帮助学生理解与记忆。比如将经济总量 GDP 看作时间的函数，我国 2023-2025年 GDP 按照 5%的趋势不断增长，当时间微小变化时，GDP的增长是相对平滑的，不会出现突然大幅度跳跃，体现了函数的连续性。

2.课堂教学

提前 1~2 天在超星学习通发布关于函数连续性的问题，如（1）生活中常常用到“连续”这个词语描述时间的流逝、河流的流动等，请举 2-3 个有关描述连续性的生活现象；（2）尝试用数学语言描述连续性；（3）请预习课本 1.6 节函数的连续性的概念，思考函数连续与函数极限精确定义的区别；（4）函数在区间连续与在一点的连续有何不同，并举例说明。

课堂学习中，根据问题的类型先进行小组讨论与互评，再由老师用词云图的方式展示学生的热点词汇，对学生的回答作出评价与分析，学生对函数连续性的概念有了基本认识。

回顾函数极限的δ-ε定义，增加函数在点 x0有定义的条件，强调函数在该点的极限值等于函数值，从而引出连续性的精确定义。举例说明反比例函数、抛物线函数、线性函数在其定义域内的每一个点处都是连续的，这类函数也叫在区间连续或叫连续函数，学生已经理解了函数在一点连续和区间连续的区别，通过小组讨论的方式，归纳出已学的函数哪些是连续函数。

进一步，请同学们思考分段函数在不同区间的连续性并讨论函数在分段点处的连续性。例如符号函数 y=sgnx 在不同区间内表现为常函数（是连续的），分段点 x=0 处不连续，因其左右极限值虽然存在但是不相等，体现了分段函数在特定点可能存在的不连续性或间断性。以小组为单位，通过举例的方式归纳函数间断点的情形并展示成果，通过学生互助评价，学生已深入理解了函数连续性的多样性与复杂性。

课堂最后进入高阶思维训练环节，引导学生探究函数连续性在实际问题中的应用，理解连续函数意味着函数图象可以一笔画出与数学定义间的关系。通过本节课程的学习，结合网络资源，学生之间互相提问并分享学习心得，进一步巩固对函数连续性的理解。

3.课后反思

教学反思是提升教学质量的重要环节，通过对课堂的整体回顾、学生参与情况和学生的信息反馈，教师进行调整教学策略，对课堂内容设计的再优化，以更好的适应学生的学习需求。反思中发现，学生对于课前的 4 个问题，参与度分别是：92%，10%，78%和 63%，针对问题（1）、（3）、（4）的参与度较高，说明学生对连续性有一定的认知基础，通过查找课本可以轻松完成（3）、（4）问题，第（2）个问题的参与度很低，结合本班学生课堂的平时表现，发现学生看到数学语言描述，一方面对数学语言表现出困惑，一方面普遍认为自己做不到，也不愿意尝试。同时在课堂中部分小组讨论热烈，能准确识别函数间断点及类型，但对复杂函数的连续性判断仍显不足。需加强数学语言理解训练，提升学生自信心，鼓励多尝试。此外，教师在课堂中的引导和示范作用有待加强，指令描述要具体清晰，避免学生因理解偏差而影响学习效果。图 1 呈现了本节课程教学设计思路。

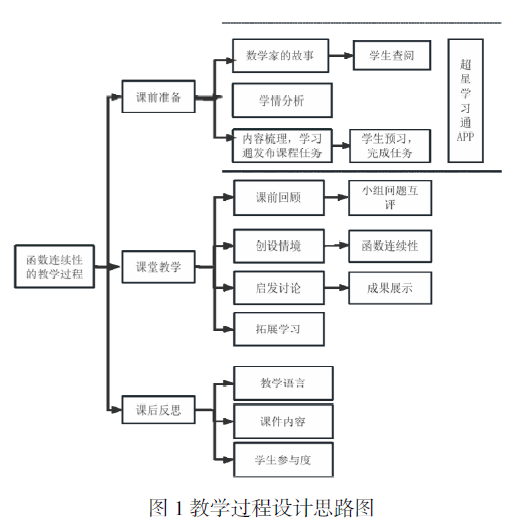
三、总结

采用线上+线下的混合式教学设计，通过实例刻画函数连续性，基于函数极限定义给出函数连续性的精确定义，再到对间断点的认识及常见函数连续性的判断，完成对函数连续性从认识-定义-理解-归纳-应用的完整闭环。参考文献：
【1】刘啸霆.科学技术与社会概论[M].北京:高等教育出版社,2008:156 -158.
【2】刘冬梅.高等数学教学的困境及解决探索[J].高教学刊,2019,25（23）:78-80.
【3】王金红.人工智能时代开放大学高等数学课程教学模式的 创 新 研 究 [J]. 中 国 多 媒 体 与 网 络 教 学 学 报 ,2023,8 （3）:65-68.
【4】黄利文,张纪平,董会英，傅瑞瑜，石擎天.基于人工智能的应用型高校高等数学课程教学改革研究[J].牡丹江教育学院学报,2024,8（264）:72-76.